Learn all about miniboxing in a 5 minute demo.


Linked List Example

This page will describe how the miniboxing plugin speeds up a linked list, which is modeled after the Scala collections immutable linked list. This page is based on the work of Aymeric Genet, submitted to SCALA’14.

The source code is included in the miniboxing-plugin sources (benchmarking code), and benchmarking the example can be done either using the miniboxing-example project or by installing the miniboxing plugin sources locally and following the instructions here.

The benchmarks show speedups between 1.5x and 4x, despite the non-contiguous nature of the linked list, so we expect even better speedups for vectors and hashmaps:


Scala Collection Patterns

In the following section presents the common patterns that enable the high-level interface in the Scala collections, and how miniboxing can be applied in order to improve performance.

Inheritance and Mixins

Inheritance and mixins group the common behavior of different collections. This reduces code duplication and gives rise to a convenient collection hierarchy, where each level of the inheritance makes more assumptions about the architecture than the previous level. For example, the path to a linked list goes through Traversable, Iterable, Seq, LinearSeq and finally List.

This nesting and splitting of functionality makes is necessary to have deep miniboxing: Adding the @miniboxed annotation to a collection type parameter will not be enough to fully transform it, as most of its functionality will be inherited from parent traits. Instead, what needs to be done is to deeply visit all the parent traits and mark their arguments as @miniboxed:

 // trait/class definition needs to be marked:
 trait Traversable[@miniboxed +A] extends
 // parents' definitions also have to be marked:
       TraversableLike[A, Traversable[A]]
       with GenTraversable[A]
       with TraversableOnce[A]
       with GenericTraversableTemplate[A, Traversable] { ... }

Since the goal of Scala collections is to avoid code duplication, collection comprehensions, such as map and filter, all rely on a common mechanism: visiting each element in the collection, performing an action for it and (optionally) adding the result to a new collection. For example, filter visits all elements and for each element applies a predicate which decides whether the element should be part of the resulting collection or not:

  // From the Scala TraversableLike trait:
  def map[B, That](f: A => B)(implicit bf: CanBuildFrom[Repr, B, That]): That = {
    val b = ...
    // after desugaring, this is a foreach loop:
    for (x <- this) b += f(x)
    b.result
  }

The two key elements necessary for implementing collection comprehensions are:

Function Encoding

In Scala, it is common to use functions to manipulate collections. For example, in order to extract the positive numbers in a List of integers, we can use the filter method along with the following function:

 List(4,-2,1).filter(x => x > 0)

However, since the Java Virtual Machine doesn’t support functions (at least not until Java 7), Scala needs to provide a special translation for them:

 List(4,-2,1).filter({
     class $anon extends Function1[Int, Boolean] {
       def apply(x: Int): Boolean = x > 0
     }
     new $anon()
   })

The Function1 trait is provided by the standard library and can’t be overridden with a miniboxed version. Hence, in order to specialize functions, we need to provide our own function traits, which are miniboxed and perform the desugaring by hand.

This is done by creating a custom MyFunc1 trait that receives two type parameters, T and R, which signal the argument and return of our function, i.e (T => R). This trait exposes an abstract apply function that will contain the actual code of the function. Miniboxing is triggered by annotating both of the type parameters with @miniboxed:

 trait MyFunc1[@miniboxed -T, @miniboxed +S] {
   def apply(t: T): S
 }

The miniboxing plugin will generate five different traits, which will be used to encode functions. These correspond to the interface plus the 4 possible combinations for the 2 representations: (erased, erased), (erased, miniboxed), (miniboxed, erased), (miniboxed, miniboxed). The transformation will also create 4 versions of the apply method:

  abstract trait MyFunc1[-T, +R] extends Object {
    def apply(t: T): R
    def apply_JL(..., t: long): R
    def apply_LJ(..., t: R): long
    def apply_JJ(..., t: long): long
  }

Then, just like methods, four different abstract traits that extend the previous interface will be created.

Now, in order to express the previous function, we can write:

 new MyFunc1[Int, Boolean] { def apply(x: Int): Boolean = x > 0 }

And the miniboxing transformation will translate this to:

 new MyFunc1_JJ[Int, Boolean] { ... }

Now, any invocation of this function will actually invoke apply_JJ, thus completely avoiding boxing primitive types, such as int and boolean.

Note that this has been addressed in the 0.4 version of the miniboxing plugin.

Builder Pattern

The Builder pattern is the key component necessary for collection comprehensions: It greatly reduces code duplication, since all the collection comprehensions reduce to creating a new collection with either transformed of filtered elements. It also brings flexibility, as shown by the following example:

scala> val map = Map(1 -> 2, 2 -> 3)
map: immutable.Map[Int,Int] = ...

scala> map.map({ case (x, y) => (y, x) })
res1: immutable.Map[Int,Int] = ...

scala> map.map({ case (x, y) => x })
res2: immutable.Iterable[Int] = ...

To achieve this, the map function will rely on a Builder generated from the CanBuildFrom parameter, where Repr is the current collection and That is the resulting collection:

  def map[B, That](f: A => B)(implicit bf: CanBuildFrom[Repr, B, That]): That = {
    val b = bf(repr) // the builder
    for (x <- this)
      b += f(x)
    b.result
  }

The Builder pattern also shows how type constructor polymorphism can play an essential role in factoring out boilerplate code without losing type safety.

Here, we need to add the miniboxed annotation to the Builder objects, which interact with primitive values to form the collection. We can get away with only miniboxing the first type parameter, which can be replaced by a primitive:

// Builder
trait Builder[@miniboxed -T, +To] {
  def +=(e1: T): Unit
  def finalise: To
}

class ListBuilder[@miniboxed T] extends Builder[T, List[T]] {
  ...
}

The CanBuildFrom object can remain generic, as it will not be involved in manipulating primitive values. Instead, its creation needs to be miniboxed:

// Can build from implicit
trait CanBuildFrom[-From, -Elem, +To] {
  def apply(): Builder[Elem, To]
}

object List {
  implicit def canBuildFrom[@miniboxed A]: CanBuildFrom[List[_], A, List[A]] =
    new CanBuildFrom[List[_], A, List[A]] {
      def apply = new ListBuilder[A]  // <= since A is miniboxed, this will also be
                                      //    creating the miniboxed version of ListBuilder
    }
}

All these explanations are derived from the optimized stack trace initiator, propagator and inhibitor rules given in the tutorial.

Numeric Pattern

Since generic type parameters can be instantiated by any type in the language, they are bounded by Any, the top type of the Scala hierarchy. Therefore, they do not define mathematical operations, such as + or *. This can be limiting when operating with numeric types.

The Numeric pattern solves this issue by allowing mathematical operations in a generic context. This is done by creating a generic Numeric trait that provides mathematical operations for a certain type. By example, one could define a way to add two numerical values, by providing such a definition to the trait:

 trait Numeric[@miniboxed T] {
   def plus(x: T, y: T): T
   ...
 }

We can extend the trait into different concrete implementations, that provide operations for each primitive type individually. This pattern also works for non-primitive number representations such as BigInteger. For instance, the code for Numeric[Int] would be:

 implicit object NumInt extends Numeric[Int] {
   def plus(x: Int, y: Int): Int = x + y
   ...
 }

Now, every time we want to use a type parameter as a numeric type, we enforce that the Numeric version of the type exists, so we can call the mathematical operations on them. Here is a complete example of a two-dimensional vector class:

 class Vec2D[T : Numeric](val x: T, val y: T) {
   def +(that: Vec2D[T]): Vec2D[T] = {
     val n = implicitly[Numeric[T]]
     new Vec2D[T](
       n.plus(this.x, that.x),
       n.plus(this.y, that.y))
   }
   ...
 }

Since the Numeric implementations are likely to use primitive type parameters, boxing and unboxing would frequently occur. This is where the miniboxing steps in. With a simple @miniboxed annotation on the type parameter of the Numeric class, a concrete extension would override an optimized version for primitive types. The classes that use the Numeric objects should also have a @miniboxed annotation. This would avoid every occurrence of boxing and unboxing, and greatly enhance the performance.

Benchmarks

To evaluate the miniboxing plugin, we implemented a mock-up of the Scala collections library and benchmarked the performance. The result: 1.5x-4x speedup just by adding the @miniboxed annotation. And it’s worth pointing out our mock-up included all the common patterns found in the library: Builder, Numeric, Traversable, Seq, closures, tuples etc.

The benchmark we ran is fitting a linear curve to a given set of points using the Least Squares method. Basically, we made a custom library and benchmarked this code:

  val xs: List[Double] = // list of x coordinates
  val ys: List[Double] = // list of y coordinates

  // list of (x,y) coordinates:
  val xys = xs.zip(ys)

  // intermediary sums:
  val sumx  = xs.sum
  val sumy  = ys.sum
  val sumxy = xys.map(mult).sum
  val sumsquare = xs.map(square).sum

  // slope and intercept approximation:
  val slope = (size * sumxy - sumx * sumy) / (size * sumsquare - sumx * sumx)
  val intercept = (sumy * sumsquare - sumx * sumxy) / (size * sumsquare - sumx * sumx)

We ran this code with two versions of the library: one with the plugin activated and one with generic classes. The numbers were obtained on an i7 server machine with 32GB of RAM, and we made sure no garbage collections occured (-Xmx16g, -Xms16g):

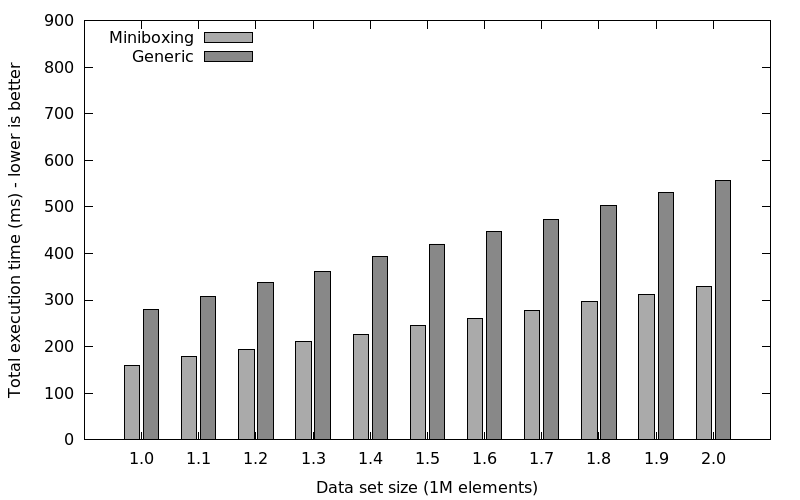
Collection size Miniboxed (ms) Generic (ms)
1000000 160 279
1100000 177 308
1200000 193 336
1300000 211 362
1400000 226 393
1500000 245 420
1600000 260 447
1700000 277 473
1800000 297 502
1900000 311 530
2000000 328 557
2100000 342 583
2200000 360 615
2300000 375 642
2400000 391 669
2500000 407 693
2600000 419 721
2700000 440 754
2800000 457 783
2900000 471 804
3000000 487 831

This shows miniboxed linked lists are 1.5x to 2x faster than generic collections, despite the fact that linked lists are not contiguous, thus reducing the benefits of miniboxing. We have also tested specialization, but it ran out of memory and we were unable to get any garbage collection-free runs above 1500000 elements (we suspect this is due to bug SI-3585 Specialized class should not have duplicate fields, but haven’t examined in depth)

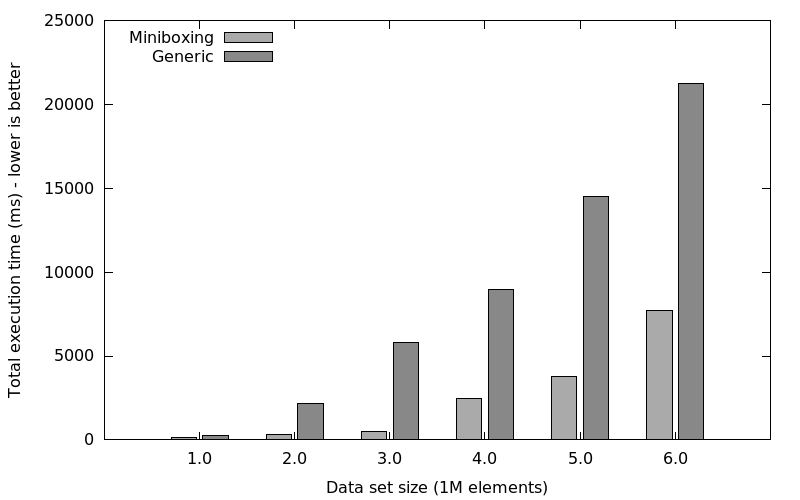
We also wanted to test how miniboxing copes with garbage collection cycles compared to the generic library. To do so, we limited the heap size to 2G (-Xmx2g, -Xms2g, -XX:+UseParallelGC):

Collection size Miniboxed (ms) Generic (ms)
1000000 163 269
2000000 327 2173
3000000 491 5830
4000000 2442 8980
5000000 3804 14502
6000000 7708 21267

To summarize, on linked lists, we can expect speedups between 1.5x and 4x, despite the non-contiguous nature of the linked list. Therefore we expect even better speedups for vectors and hashmaps, which use underlying arrays for values.

Try it yourself!

The source code is included in the miniboxing-plugin sources (benchmarking code), and benchmarking the example can be done either using the miniboxing-example project or by installing the miniboxing plugin sources locally and following the instructions here.

Important: Don’t forget the -P:minibox:two-way flag when compiling the example!

Comments

Comments are always welcome! But to make the best use of them, please consider this:

Thanks! Looking forward to your messages!


comments powered by Disqus