Miniboxed Scala Functions
This page describes how the miniboxing plugin transforms higher-order functions to avoid boxing.
Executive summary: starting version 0.4 of the plugin, miniboxed code is capable of invoking Scala functions, such as (x: Int) => x + 1 without boxing the argument and the returned value.
- Advantages:
- no need to define custom function representations in order to invoke them without boxing
- seamless integration with the standard Scala library
- Disadvantages:
- a small but pervasive overhead of 10%-20% when invoking functions:
Motivation
The miniboxing plugin aims at maintaining the high-level nature of the Scala programming language while eliminating the cost of abstraction in terms of running time for generics. Since Scala marries the functional programming style and object-orientation, in the Scala world, functions are objects and objects can be functions. Expressing the types of a function’s arguments and its return type is done using generics, so this leads to a natural question:
Can higher-order functions be optimized by miniboxing too?
The answer so far has been NO, since functions have a fixed representation implemented in the Scala standard library, and, for reasons described here it is not possible for miniboxing to directly optimize functions.
Now, version 0.4 of the miniboxing plugin automatically optimizes functions, and the results are really cool!
Mechanism
Previous miniboxing plugin versions required defining your own function representation to avoid boxing:
trait MyFunc1[@miniboxed -T, @miniboxed +S] {
def apply(t: T): S
}With a custom function representation, the miniboxing plugin was able to transform both the function representation and the caller code to completely avoid boxing value types. Yet, this forced programmers to perform desugaring by hand. For example, instead of writing (x: Int) => x + 1, they would have to write:
new MyFunc1[Int, Int] {
def apply(t: Int): Int = x + 1
}What a waste! So why exactly was miniboxing unable to improve standard Scala functions? Because standard functions are compiled without the miniboxing compiler plugin – even worse, they’re compiled with the incompatible specialization transformation (see this bug for reference).
Now, since version 0.4, the miniboxing plugin, standard Scala functions can be efficiently used by miniboxed code. To get there, the miniboxing plugin now introduces three tweaked versions of the function representation for 0, 1 and 2 arguments:
package miniboxing.runtime
trait MiniboxedFunction0[@miniboxed +R] {
def f: Function0[R]
def apply(): R
}
trait MiniboxedFunction1[@miniboxed -T1, @miniboxed +R] {
def f: Function1[T1, R]
def apply(t1: T1): R
}
trait MiniboxedFunction2[@miniboxed -T1, @miniboxed -T2, @miniboxed +R] {
def f: Function2[T1, T2, R]
def apply(t1: T1, t2: T2): R
}It automatically wraps standard Scala functions into MiniboxedFunctions and modifies the signatures of methods to use them:
$ cat func.scala
object Test {
val f: Function1[Int, Int] = (x: Int) => x
f(3)
}
$ mb-scalac func.scala -Xprint:minibox-commit
[[syntax trees at end of minibox-commit]] // func.scala
package <empty> {
object Test extends Object {
...
val f: miniboxing.runtime.MiniboxedFunction1[Int,Int] = ... // <= notice the type change:
// Function1 => MiniboxedFunction1
def f(): miniboxing.runtime.MiniboxedFunction1[Int,Int] = Test.this.f
f().apply_JJ(int2minibox(3))
}
}The fact that the last line calls apply_JJ means that the argument and return type are miniboxed, thus optimized. On the other hand, how exactly does the bridging between Function and MiniboxedFunction take place?
We won’t go into details, but here is how Scala would normally encode f, without the miniboxing plugin:
val f: Function1[Int,Int] = {
@SerialVersionUID(0) final <synthetic> class $anonfun extends
scala.runtime.AbstractFunction1[Int,Int] with Serializable {
...
final def apply(x: Int): Int = x
}
new <$anon: Int => Int>(): Int => Int)
}The block defines an anonymous class $anon which extends the Function1 trait and implements the apply method. Now,
when the miniboxing plugin is active, this is:
val f: miniboxing.runtime.MiniboxedFunction1[Int,Int] = {
@SerialVersionUID(0) final <synthetic> class $anonfun extends
scala.runtime.AbstractFunction1[Int,Int] with Serializable {
...
final def apply(x: Int): Int = x
}
MiniboxedFunctionBridge.this.function1_opt_bridge_long_long[Int, Int]( // <== added wrapper
5, 5, (new <$anon: Int => Int>(): Int => Int)) // around the function
}But what exactly does the MiniboxedFunctionBridge.this.function1_opt_bridge_long_long method do? It actually transforms the instance of Function1 into a MiniboxedFunction1:
def function1_opt_bridge_long_long[T, R](T_Tag: Byte, R_Tag: Byte, _f: Function1[T, R]):
MiniboxedFunction1[T, R] =
((T_Tag + R_Tag * 10) match {
case 55 /* INT + INT * 10 */ =>
val _f_cast = _f.asInstanceOf[Function1[Int, Int]]
new MiniboxedFunction1[Int, Int] {
def f: Function1[Int, Int] = _f_cast
def apply(arg1: Int): Int = _f_cast.apply(arg1)
}
...
case _ =>
function1_bridge(_f)
}).asInstanceOf[MiniboxedFunction1[T, R]]This doesn’t look very optimal, but oh it is! After compiling and letting both miniboxing and specialization do their magic, the case actually looks like (warning: heavily simplified):
case 55 =>
val _f_cast = _f.asInstanceOf[Function1[Int, Int]]
new MiniboxedFunction1_JJ[Int, Int](INT, INT) {
def f: Function1[Int, Int] = _f_cast
...
def apply_JJ(T_Tag: Byte, arg1: Long): Long = // callee for miniboxed sites => no boxing
_f_cast.apply$mcII$sp(long2int(arg1)) // call to specialized code => no boxing
}The bridge basically wraps the Function1 in a MiniboxedFunction1, offering a call site where miniboxing can call
and which, when called, invokes the specialized variant, thus avoiding boxing completely. This is the change necessary
for the miniboxing plugin to avoid boxing when calling functions.
The key insight is that once the MiniboxedFunction1 was created, there is no dispatching overhead – the class created
knows exactly how to call the specialized function code, such that it avoids boxing. Alternative approaches, such as
changing the apply method to a special call would actually perform the match on each invocation, significantly
slowing down execution.
Of course, this also comes with a couple of drawbacks:
- an additional call from miniboxing into specialized code: instead of the caller calling
apply$mcII$spdirectly, it has to go throughapply_JJ; - since
FunctionXclasses are not specialized for all primitives and are not partially specialized (either both the argument and return are primitives or both are generic, all or nothing), not allMiniboxedFunctionX-es have corresponding optimizedapply$mcXY$spmethods to call; - this creates an additional heap object for each function – while this is not a huge issue, it does become important when dealing with many closures, as their memory footprint increases.
Interoperation
How does this code interoperate with the previous representation? Let us take the following example:
Set(1,2,3).map(f)where f was defined earlier and is of type MiniboxedFunction1[Int, Int]. The Set collection is the immutable Set
from the Scala library. It is compiled without the miniboxing plugin, therefore its signature expects a Function1 and
not a MiniboxedFunction1. How does the miniboxing plugin transform this?
Well, when a MiniboxedFunctionX is given and FunctionX is expected, since miniboxed functions wrap functions, it’s just
a matter of extracting the FunctionX:
Set(1,2,3).map(f.f() /* defined by the bridge as "def f: Function1[Int, Int]" */)This said, let us see how this mechanism performs in practice.
Benchmarks
We performed the benchmarks on the least squares method implemented using a mockup of the Scala immutable linked list implemetation:

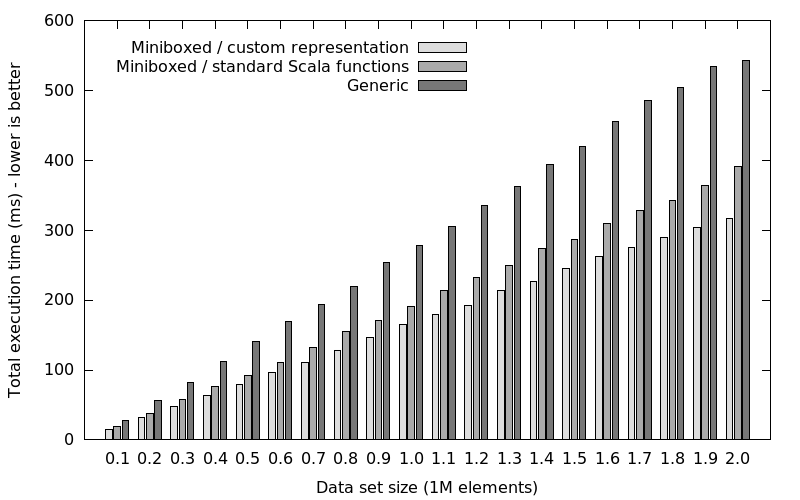
In the graph, the following scenarios are shown:
Miniboxed / custom representation- custom function representation instead of Scala’s
FunctionX - requires manual desugaring for all higher-order functions
- described in the linked list example
- is typically 45% faster compared to
genericfor the linked list example
- custom function representation instead of Scala’s
Miniboxed / standard Scala functions- programmer uses the standard
FunctionXrepresentation or theX => Ysynthetic sugar - no need for manual desugaring,
(x: Int) => x + 1is automatically desugared by the compiler - thanks to the improved translation, invoking functions does not require boxing (*in most cases)
- introduces a 15% overhead compared to the
custom functions(for the linked list example) - is typically 30% faster compared to
generic(for the linked list example)
- programmer uses the standard
Generic- the generic version of the benchmark which we all know and hate
The numbers (raw data avaialable here):
| Collection size | Miniboxed / custom functions (ms) | Miniboxed / library functions (ms) | Generic (ms) |
|---|---|---|---|
| 100000 | 15 | 19 | 27 |
| 200000 | 31 | 38 | 55 |
| 300000 | 48 | 57 | 82 |
| 400000 | 63 | 76 | 112 |
| 500000 | 79 | 91 | 140 |
| 600000 | 96 | 110 | 169 |
| 700000 | 110 | 132 | 193 |
| 800000 | 128 | 155 | 219 |
| 900000 | 145 | 170 | 253 |
| 1000000 | 165 | 191 | 277 |
| 1100000 | 179 | 214 | 305 |
| 1200000 | 192 | 232 | 335 |
| 1300000 | 213 | 250 | 362 |
| 1400000 | 226 | 273 | 393 |
| 1500000 | 244 | 286 | 419 |
| 1600000 | 262 | 309 | 456 |
| 1700000 | 275 | 328 | 485 |
| 1800000 | 290 | 342 | 503 |
| 1900000 | 303 | 364 | 534 |
| 2000000 | 317 | 391 | 542 |
Conclusions:
This article presents the mechanism implemented in miniboxing to allow efficient interoperation with higher-order functions using the standard Scala object-oriented representation. There are three take home points:
- defining and maintaining custom function representations is not practical and does not scale, so it requires automation
- automation is implemented in the miniboxing plugin with limited overhead
- the new implementation has technical issues you should be aware of:
Comments
Comments are always welcome! But to make the best use of them, please consider this:
- If you have questions or feedback regarding the content of this page, please leave us a comment!
- If you have general questions about the miniboxing plugin, please ask on the mailing List.
- If you found a bug, please let us know on the github issue tracker.
Thanks! Looking forward to your messages!
comments powered by Disqus


